OSCILACIONES FORZADAS
La amplitud de una oscilación amortiguada decrece con el tiempo. Al cabo de un cierto tiempo teóricamente infinito, el oscilador se detiene en el origen. Para mantener la oscilación es necesario aplicar una fuerza oscilante.
El oscilador forzado, o su equivalente el circuito LRC conectado a una fuente de corriente alterna es un ejemplo que nos permite estudiar con detalle las soluciones de una ecuación diferencial de segundo orden. Nos permite diferenciar entre estado transitorio y estacionario. Comprender el importante fenómeno de la resonancia
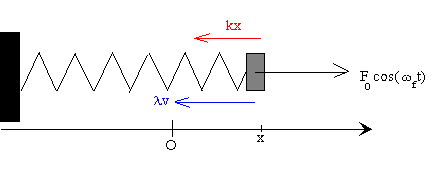
Las fuerzas que actúan sobre la partícula son:
-
La fuerza que ejerce el muelle, -k·x
-
La fuerza de rozamiento proporcional a la velocidad λv y de sentido contrario a ésta
-
La fuerza oscilante F0·cos(ωf t) de frecuencia angular ωf
La ecuación del movimiento de la partícula es
ma=-kx-λv+F0·cos(ωf t)
Expresamos la ecuación del movimiento en forma de ecuación diferencial que describe las oscilaciones forzadas

-
donde ω0 es la frecuencia natural o propia del oscilador
-
ωf es la frecuencia angular de la fuerza oscilante de amplitud F
-
γ es la constante de amortiguamiento, γ<ω0
La solución general de la ecuación diferencial homogénea tiene la forma
Donde los coeficientes C y D se determinan a partir de las condiciones iniciales
Supondremos inicialmente que ω0≠ωf
Una solución particular de la ecuación diferencial completa tiene la forma
x2=Acos(ωf t)+Bsin(ωf t)
Obtendremos los valores de A y B haciendo que cumpla la ecuación diferencial lineal completa





PROGRAMACION